Introduction to Logic

CHAPTER 11. INDUCTION

11. INDUCTION
a) Simple Enumeration as a form of induction.
b) Analogy – characteristic of a good and bad analogy.

c) Use of simple enu,eration and analogy in law – circumstantial evidence.

Induction is a type of inference where we go from known to unknown or from less general to more general. Here, from the things that are known, we say something about things that are not known. This is the reason why in induction we always say something more than what we already know of.

So, Induction, a form of argument in which the premises give grounds for the conclusion but do not make it certain. Induction is contrasted with deduction, in which true premises imply a definite conclusion, the conclusion of Induction is always probable. The probability rate changes as per strength of evidence.

Unlike deductive arguments, inductive reasoning allows for the possibility that the conclusion is false, even if all of the premises are true.

Induction is of two types, perfect and imperfect. Perfect induction takes support of deduction in later stages to establish a certain conclusion, while imperfect induction does not do this.

The two types of imperfect induction are, Simple enumeration and Analogy.

a) Simple Enumeration as a form of induction.

Simple enumeration is a method of arriving at a generalization on the basis of uniform uncontradicted observation of something.

While using this method, we observe a number of instances that agree in some quality. During our observation, we do not find any contrary instance. So, we arrive at a conclusion that as far as that thing is concerned, there are no contrary instances. Then we get a general proposition as a conclusion.

We do not verify our conclusion further or try to analyze the events in order to find any logical relationship in these common similar events.

This is the reason why even when our observation is wide, it still stays imperfect. This is because our method is a method of SIMPLE enumeration and not COMPLETE enumeration. In complete enumeration, since we have observed all instances from a group about which we are talking, there is no chance of coming across a contrary instance. But this is not the condition of simple enumeration.

In simple enumeration, conclusion can be disproved by observing just one single contrary instance. So, wider the observation, greater is the probability of an inference by simple enumeration.

The conclusion by simple enumeration is highly probable when the number of observed instances is really high.

But if one is arriving at a conclusion on the basis of very limited observation, the conclusion is less probable and hence, it is termed as hasty generalization or illicit generalization.

Many times we find that people arrive at hasty generalizations in determining some vital things in their daily life.

b) Analogy –

Analogy is a type of imperfect induction where we are comparing two things, persons, groups or classes. while doing so, we observe some similarities and on the basis of these, we infer some further similarity, as we find an additional quality in one of the two compared things, persons, groups or classes.

Many times, we observe or compare two things, events, groups, individuals, things, etc. etc, observe some similarities, and then, infer some further similarity. We have no logical reason why we get such a conclusion, but we simply rely on our observation. This is how analogy works.

Characteristic of a good and bad analogy.

Here, if the observed similarities are relevant to the additional quality, then our conclusion is likely to be true and we may say that Analogy is good Analogy.

But if the observed qualities are not relevant to the additional quality, then our conclusion about predicting the additional similarity is not likely to be true, so, we say that such an analogy is Bad Analogy.

c) Use of Simple Enumeration and Analogy in law:

in circumstantial evidence & getting precedents.

In law, we need to use simple enumeration and Analogy to infer things from circumstantial evidence. Of them analogy is more useful in legal matters. Also, while using precedent law, we use analogy to indicate the support of past decided cases in our matter.

When we see a person following some pattern of behavior or thinking or actions, while talking of the Modus Operandi of that person, we use simple enumeration as we talk of the generalized pattern of behavior of that person.

This is the method followed by criminal investigators quite often.

They determine the Modus Operandi of a criminal to find out the criminal and / or to track the criminals. This is a very common practice used by the police in registering the crime record of certain criminals while maintaining their files.

While contesting any matter, the lawyers use analogy in arguing about similar matters, or actions done by an individual in similar situations, to infer about the truth of the statement given by any witness.

For example, if it is shown that the witness had reacted in a particular way in the past in similar situations, or has reacted in a particular way in similar situation created in court, then, one can infer that he must have reacted exactly in same way when the actual event had happened that the witness was witnessing.

This type of inference adds to the weight-age in argument in court.

Similarly, when we are arguing any matter, we may come across previously decided matters of same type in the same court, or higher court or another court. We use the citation of these matters as case law or precedent law to lead the judge to the conclusion we want, and the procedure of inductive argument that we use in this type of matter is of analogy. This is why is is said that Analogy is of great use in legal arguments.

CHAPTER 10. DIVISION

10. DIVISION
Logical division - rules and fallacies of division - division by dichotomy.

Logical division:

Logical division is a simple method of dividing a class into its sub-classes in order to explain the or describe any class. This type of division is useful in explaining many concepts and making the understanding clear.

Division is useful for;

a] determination of exact relationships among related things,

b] formulation of definitions

When we divide, we use two main criteria. These are, Physical division and metaphysical division.

Physical division divides a whole into its parts
• e.g., a complex machine into its simple mechanical parts

Metaphysical division divides an entity into its qualities,

• e.g.,a species into its genus & difference
– man into animality & rationality

• a substance into its attributes
– sugar into color, texture, solubility, taste, etc.

• a quality into its dimensions
– sound into pitch, timbre, volume

Understanding Division:

Division is another way to explain any class by talking about its sub-groups and dividing the class into its sub groups. Here are its basic qualities:

• Logical Division

– begins with a summum genus
– proceeds through intermediate genera
– ends at the infimae species
– NB: It does not continue to individuals

• The results of division should meet these criteria:

1. The subclasses of each class should be coextensive with original class.
2. The subclasses of each class should be mutually exclusive.
3. The subclasses of each class should be jointly exhaustive.
4. Each stage of a division should be based on a single principle.

Kinds of Classification

Classification is the technique of inquiry in which similar individuals and classes are grouped into larger classes.

e.g., how are steam, diesel, & gasoline engines related to one another?

Natural Classification:
• Natural classification is a scheme that provides theoretical understanding of its subject matter e.g. classification of living things into monerans, protistans, plants, fungi and animals
• The concept “monerans” is now obsolescent because it does not provide sufficient theoretical clarity.

Artificial Classification:
• Artificial classification is a scheme established merely to serve some particular human purpose e.g. classification of plants as crops, ornamental, and weed

Classification and Division Compared

• The result of a classification will look like the result of a division.
• Classification begins with a individuals or small classes and works
towards a summum genus. It works in the direction opposite to that of division
• Classification begins with a set of apparently related things found in
the world based on experience and builds from there. Hence, it is well-suited to natural objects. But it will work with any kind of object.

Two Overly Ambitious Ideals

the divisions by a few things can never encounter any fallacy.

In logic as well as in any reasoning, if we are using division to explain something, we all aim at making divisions that will have no fallacies. In order to have a perfect flawless division we must divide using one of the following methods.

• Pure division
– begins with the summum genus and
– divides on the basis of a priori considerations
• i.e., it is based on logical possibility, not experience

• Dichotomous division
– divides on the basis of the presence or absence of a particular feature
• Classification can also be dichotomous.
• Striving for these ideals
– works well with mathematical objects,
– does not work well with natural objects
– guarantees a division that meets criteria
– sometimes provides more insight than alternative divisions.
• But “ dichotomous division is often difficult and often impracticable”
• Sometimes, class Rules notification is more practical.

RULES OF DIVISION:

When we are using logical division, we need to follow certain rules. thesde are as follows:

1. One division must follow only one criteria. It must be either physical or metaphysical.
2. The division criteria must be mutually exclusive and collectively exhaustive.
3. All the parts of an entity being explained must be covered by the division.
4. No extra members must be suggested as parts of the entity explained during the process of division.

FALLACIES OF DIVISION:

When we fail to follow above rules, we end up in committing following fallacies:

1. Division by cross criteria: When we divide something by using two or more criteria at the same time, we commit this fallacy. e.g. when we divide Indians into "Hindus, Muslims, Christians, Sikh, Rich, poor, Tall, short, Fair, Dark, introverts and extroverts"; we are committing this fallacy as we are using many criteria, both of physical as well as metaphysical divisions at the same time. at the same time.
2. Too narrow division: when we exclude some of the members from the group or some qualities of the entity being explained, we commit this fallacy. e.g. Quadrilateral into, square and rectangle. Here we exclude many other types of quadrilaterals and so the division becomes too narrow as it leaves out many other members that actually belong to this group.
3. Too wide division: when we include some members that actually do not belong to the group as we are dividing, our division becomes too wide. e.g. birds into single coloured & multicolored. Here, many other single coloured and multicolored things and beings get indicated as part of the group of bird, so it is a too wide division.

CHAPTER 6. INFERENCE

6. INFERENCE
a) Kinds of inference- Immediate and Mediate.
b) Opposition of proposition- Types of opposition- inference by opposition of propositions- opposition of Singular propositions.

AN INFERENCE is a mental process by which we pass from one or more statements to another that is logically related to the former.

a) Kinds of inference –

Inferences are classified on the basis of their scope into Deductive and Inductive. Deductive Inference have a conclusion that stays within the scope of premises. Inductive Inferences are the ones that go beyond the scope of the premises.

The Deductive Inferences are of two types, Mediate and Immediate.

Inductive Inferences are of two types, perfect induction and imperfect induction.

Immediate & Mediate

We are studying the Immediate and mediate inferences here.

Based on the number of their premise, inferences are basically classified into two types, immediate and mediate:

Immediate Inference consists in passing directly from a single premise to a conclusion. It is reasoning, without the intermediary of a middle term or second proposition, from one proposition to another which necessarily follows from it.

Ex: No Dalmatians are cats. Therefore, no cats are Dalmatians.

All squares are polygons. Therefore, some polygons are squares.

Mediate Inference consists in deriving a conclusion from two or more logically interrelated premises. Involving an advance in knowledge, it is reasoning that involves the intermediary of a middle term or second proposition which warrants the drawing of a new truth.

Ex: All true Christians are theists.

Paul is a true Christian.

Therefore, Paul is a theist.

Let us see the various types of inferences and their sub classes:

The following outline serves as a guide in understanding the different types of inference according to various classifications.

I. Induction

A. Perfect Induction

B. Imperfect Induction

II. Deduction

A. Immediate Inference

1. Oppositional Inference

a. Contrary Opposition

b. Contradictory Opposition

c. Subaltern Opposition

d. Subcontrary Opposition

2. Eduction

a. Obversion

b. Conversion

c. Contraposition

d. Inversion

3. Possibility and Actuality

B. Mediate Inference

1. Categorical Syllogism

2. Hypothetical Syllogism

a. Conditional Syllogism

b. Disjunctive Syllogism

c. Conjunctive Syllogism

3. Special Types of Syllogism

a. Enthymeme

b. Epichireme

c. Polysyllogism

d. Sorites

e. Dilemma

b) Opposition of proposition –

Opposition of propositions is the traditional way to classify general propositions into four types on the basis of their quality and quantity. We have already discussed this in details in earlier chapters.

Types of opposition –

The opposition relation is of three types.

And we have the oppositions on the basis of

quality = Contrary [ A-E] & sub-contrary [I-O], or

quantity = sub-altern [A-I, E-O] or

both = contradictory [A X O, E X I]

Inference by opposition of proposition –

Opposite or Opposed Propositions Are propositions that cannot be simultaneously true or that cannot be simultaneously false, or that cannot be either simultaneously true or simultaneously false.

This impossibility of being simultaneously true, or false, or either true or false is the essential note of logical opposition.

Propositions are opposed if they have the same subject and predicate but differ from one another in quality or quantity, or both in quality and quantity.

When we draw the opposite of any type as a conclusion on the basis of a proposition that is known, we have an inference by opposition of proposition.

The truth functional relationship between oppositions can help us know how this relation can be effective.

Let us see the table of truth and falsity of opposition relations:

Original || Result → V	A	E	I	O
A	T / F	F / T	T / ?	F / T
E	F / ?	T / F	F / T	T / ?
I	? / F	? / T	T / F	? / T
O	F / T	? / F	? / T	T / F

Using the above table, we can infer the valid conclusions for the inferences based on the opposition relations of propositions.

Opposition of singular propositions

Singular proposition is the proposition having a singular term as its subject. In the four fold classification, this is treated as a universal proposition.

But the only difference is that unlike the general propiositions, the singular propositions do not have subalterns and contradictories. They have only contraries.

So, when we have an opposition relation of an affirmative singular proposition, taken as A, we get an E proposition. But we do not have any other variations in it.

Similarly, when we have an opposition relation of a negative singular proposition, taken as E, we get an A proposition. But we do not have any other variations in it.

This is known as opposition of singular propositions.

CHAPTER 5. COMPARATIVE STUDY OF TRADITIONAL & MODERN CLASSIFICATION

5. COMPARATIVE STUDY OF TRADITIONAL AND MODERN CLASSIFICATION OF PROPOSITIONS
a) Distinction between the Traditional and Modern General propositions.
b) Meaning of prediction with special reference to the Copula.
c) Failure of Traditional classification of propositions.

a) Distinction between the Traditional and Modern General propositions.

According to Traditional Logic general propositions are classified in four categories.

These are:

A = Universal affirmative

E = Universal negative

I = Particular affirmative

O = Particular negative

We have already studied them in details in earlier chapters.

General Propositions in modern Logic are similar to those in traditional logic.

‘All mobile phones are electronic gadgets’ is simple proposition. In such proposition we find the relation of different classes.

In the above proposition the subject term refers to a class of objects ‘mobile phones’ & the predicate term refers to another class of objects ‘electronic gadgets’.

So, a general proposition is a proposition which asserts that one class is wholly or partly included in or excluded from another class.

A general proposition, therefore, makes an assertion about all or about some of the members of a class.

The method of symbolizing with Quantifiers, seen in chapters above is actually the method used in Modern Logic, after the concept of symbolizing the propositions became popular.

b) Meaning of prediction with special reference to the Copula.

Traditional logicians have divided propositions into singular and general. Singular propositions have a single individual as a subject. This means, in a singular proposition, the subject is a singular individual thing and predicate is a class of individuals.

General propositions have a group of individuals as a subject. This means, in a General proposition, we have a group of individuals as a subject as well as a group of individuals as a predicate.

The general propositions are of two types, universal and general.

When the general proposition says something about the entire group indicated in the subject, it is known as a universal proposition.

When the general proposition says something about a part of the group indicated in the subject, it is known as a particular proposition.

Both singular and general propositions are either affirmative or negative. When we are told that the subject has the quality indicated in the predicate, the proposition is said to be affirmative. When we are told that the subject does not have the quality indicated in the predicate, the proposition is said to be negative.

In case of affirmative propositions, in singular proposition, the quality indicated in the group stated in the predicate is applicable to the individual indicated in the subject, while in general proposition, it either is applicable to the entire group indicated by the subject, as in universal propositions, or to a part of the group indicated by the subject, as in particular propositions.

In case of negative propositions, in singular proposition, the quality indicated in the group stated in the predicate is not applicable to the individual indicated in the subject, while in general proposition, it is either not applicable to the entire group indicated by the subject, as in universal propositions, or not applicable to a part of the group indicated by the subject, as in particular propositions.

According to this, the general propositions are classified into four categories.

These are:

A = Universal affirmative

E = Universal negative

I = Particular affirmative

O = Particular negative

c) Failure of Traditional classification of propositions.

The problem of multiple generality names a failure in traditional logic to describe certain intuitively valid inferences. For example, it is intuitively clear that if:

“Some cat is feared by every mouse”

then it follows logically that:

All mice are afraid of at least one cat

The syntax of traditional logic (TL) permits exactly four sentence types:

"All As are Bs",

"No As are Bs",

"Some As are Bs" and

"Some As are not Bs".

Each type is a quantified sentence containing exactly one quantifier.

Since the sentences above each contain two quantifiers; 'some' and 'every' in the first sentence and 'all' and 'at least one' in the second sentence, they cannot be adequately represented in TL.

The best TL can do is to incorporate the second quantifier from each sentence into the second term, thus rendering the artificial-sounding terms 'feared-by-every-mouse' and 'afraid-of-at-least-one-cat'. This in effect "buries" these quantifiers, which are essential to the inference's validity, within the hyphenated terms.

Hence the sentence "Some cat is feared by every mouse" is allotted the same logical form as the sentence "Some cat is hungry". And so the logical form in TL is:

Some As are Bs

All Cs are Ds

which is clearly invalid.

The first logical calculus capable of dealing with such inferences was Gottlob Frege's Begriffsschrif, the ancestor of modern predicate logic, which dealt with quantifiers by means of variable bindings.

Modestly, Frege did not argue that his logic was more expressive than extant logical calculi, but commentators on Frege's logic regard this as one of his key achievements.

Using modern predicate calculus, we quickly discover that the statement is ambiguous.

Some cat is feared by every mouse

could mean

Some cat is feared by every mouse, i.e.

For every mouse m, there exists a cat c, such that c is feared by m,

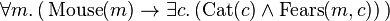
in which case the conclusion is trivial.

But it could also mean Some cat is (feared by every mouse), i.e.

There exists one cat c, such that for every mouse m, c is feared by m.

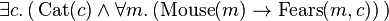
This example illustrates the importance of specifying the scope of quantifiers as for all and there exists.

CHAPTER 4. MODERN CLASSIFICATION OF PROPOSITIONS

4. MODERN CLASSIFICATION OF PROPOSITIONS
a) Aim of Modern classification, kinds of Simple and Compound propositions

b) Basic Truth Tables for Compound propositions.

Traditional logic deals with limited types of propositions. So, it was difficult to deal with many types of propositions. This is the reason why Modern Logic or formal logic came into existence. It follows and expands on Logic given by Aristotle.

This logic simplifies the way in which we reason. It also makes difference between form and content of propositions and arguments. This logic has introduced mathematical formal methods in logic and with the help of these methods, we can test the valid relationships between terms and propositions in no time.

Let us see the modern classification and its details:

a) Aim of Modern classification,.

Modern logic aims at re-organizing the logical concepts and expanding the boundaries of logical thinking. While doing so, we look at the statements used in logic with a different perspective.

This is the reason why we classify them a bit differently here on the basis of terms, verbs and connectives used in them. This way to classify the propositions makes it easy to understand the relationship between parts of the propositions in an argument as here we make them have objective and mathematical appearance.

Modern classification tries to simplify our thinking and also organize it more effectively so that more types of reasoning can be included in the classification.

Kinds of Simple and Compound propositions & basic Truth Tables

In modern logic, simple proposition is defined as one with only one verb in it. Such a proposition has no connective in it. The simple proposition have no connective. They have only one verb and do not indicate any complicated meaning.

The Simple propositions are classified into two types,

a) subject-less propositions, b) subject-predicate propositions,

The subject-predicate propositions are further classified into

i) relational propositions and ii) class membership proposition.

Let us see the simple proposition types in details:

a) Subject-less propositions, are propositions that have only predicate and no subject. These are symbolized by using single alphabet that stands for predicate.

b) Subject-predicate propositions, are the propositions that have a subject, a predicate and a verb. The subject-predicate propositions are further classified into two types. Relational and class-membership. Let us see these types:

i) Relational propositions are the propositions that show some type of relationship between the term of subject and that of predicate. This means in this type, both the subject and predicate are singular terms.

ii) Class membership proposition shows that the subject term belon gs to the class indicated by predicate. So, here, predicate term is general.

Modern logic also defines a compound proposition that has one or more components connected using one or more connectives.

The compound propositions have at least one connective used in them. They have one or more component that connectives join meaningfully.

When we express these propositions in an objective way, we can explicitly state whether the given compound proposition is true or not on the basis of truth or falsity of the components it connects and the type of connective used.

In modern logic the connecting words, commonly called as connectives, are classified into two types, viz. Monadic and Diadic.

Monadic connective is a connective that works on only one proposition.

The class of monadic connectives has only one connective in it.

This is negation.

This means in modern logic, negative proposition is no more with different quality.

It is a compound proposition.

A negation is expressed by words like 'no, never, not' etc.

While symbolizing a negation, we use the symbol ' ~ ' that is called curl or tilde.

A negation is true when the component to which it is attached is false.

Diadic connectives are connectives that work on two propositions. We have four diadic connectives. They are; conjunction, disjunction, implication and equivalence.

Conjunction is expressed by words like 'and, but'.

While symbolizing this, we use the symbol ' . ' called a dot.

A proposition with conjunction is true only when both its components are true.

Dis-junction is expressed by words like 'either, or.'

While symbolizing this, we use the symbol ' v ' called a vedge.

A proposition with disjunction is false only when both its components are false.

Implication is expressed by words like 'If...then, unless...'

While symbolizing this, we use the symbol ' ' called a horse-shoe.

A proposition with implication is false only when its antecedent, i.e. the first component is true and the consequent, i.e. the second component is false.

Equivalence is expressed by words like 'if and only if... then.'

While symbolizing this, we use the symbol ' ' called a dot.

A proposition with conjunction is true only when both its components are true.

Let us see this classification at a glance:

Proposition

Sentence that asserts

|

| |

Simple Compound (with connective)

No connective one or more components

| |

| | | |

Subject-less Subject-predicate Monadic Diadic

No subject | one component two component

| | …........................|

| | Negation 1 = Conjunction = .

Relational Class-membership =No, Not 2 = Dis junction = V

= ~ 3 = Implication =

4 = Equivalence=

b) Basic Truth Tables for Compound propositions

We saw the connectives and their symbols. Now let us see how the propositions are symbolized in modern classification.

Compound propositions are symbolized in modern classification by taking a capital alphabet for the first letter of the predicate of first component simple statement, and a capital alphabet for the first letter of the predicate of the second component simple statement.

Between these two alphabets, we put the symbol for the connective that is connecting these two components.

This means, if we have a proposition,

'If Logic is easy, then many will learn it.'

we take 'E' for 'logic is easy' and ' L' for 'many will learn it'.

The connective here is implication. The symbol for it is, .

We write this in between E and L. This reads as 'E L'

This is how we can symbolize any given proposition in modern logic.

So, if we take standard alphabets P for first component and Q for second, we can express all compound proposition types as follows:

Negation: ~P

Conjunction: P . Q

Dis-junction: P v Q

Implication: P Q

Equivalence: P Q

The method we use to check the validity of their relations is called the method of constructing truth tables. While doing this, we check the possibilities of truth and falsity in both the components.

We arrange these possibilities here using the 2ⁿ method of calculating the possibilities. Here 2 stands for the two truth value options, viz. True and false. The alphabet 'n' stands for number of variables present in the compound proposition.

If a proposition has only one variable, that means only one simple proposition, even if it is repeated, then we have 2¹ = 2 possibilities of truth value combinations.

If a proposition has two different simple statements as components, then we have 2² = 4 possibilities of truth value combinations.

If a proposition has three different simple statements as components, then we have 2³ = 8 possibilities of truth value combinations.

If a proposition has four different simple statements as components, then we have 2⁴ = 16 possibilities of truth value combinations.

Of course, for learning the basic truth-functional tables, we need to see only the first two options, i.e. the statements with 2 and 4 combination options.

When we have a single component as in ~P, we write the truth table as:

P ~P

T F

F T

When we have two components as in P . Q, P v Q, P Q, P Q, we make the truth tables by using the terms of validity of each connective as follows:

Let us write possibilities for all proposition types together for easy understanding.

P Q P . Q P v Q P Q P Q

T T T T T T T T T T T T T T

T F T F F T T F T F F T F F

F T F F T F T T F T T F F T

F F F F F F F F F T F F T F

On the basis of the above table, we can pick up the table for any relavent proposition type to be symbolized and form a truth table for it.

While doing this, follow the following steps:

Write the first part of 'P Q' and the truth values under it

then write the proposition type as per the connective.

Like,

Negation: ~P

Conjunction: P . Q

Dis-junction: P v Q

Implication: P Q

Equivalence: P Q

Then form the relevant truth table for it.

Suppose we have a proposition like, 'Law is useful and Religion is peaceful”

We symbolize it as 'U . P' Then we form a truth table for it as:

U P U . P

T T T T T

T F T F F

F T F F T

F F F F F

Suppose we have a proposition like, 'Law is useful or Religion is peaceful”

We symbolize it as 'U v P' Then we form a truth table for it as:

U P U v P

T T T T T

T F T T F

F T F T T

F F F F F

Suppose we have a proposition like, 'If Law is useful then Religion is peaceful”

We symbolize it as 'U P' Then we form a truth table for it as:

U P U P

T T T T T

T F T F F

F T F T T

F F F T F

Suppose we have proposition, 'If & only If Law is useful then Religion is peaceful”

We symbolize it as 'U P' Then we form a truth table for it as:

U P U P

T T T T T

T F T F F

F T F F T

F F F T F