CHAPTER 5. COMPARATIVE STUDY OF TRADITIONAL & MODERN CLASSIFICATION

5. COMPARATIVE STUDY OF TRADITIONAL AND MODERN CLASSIFICATION OF PROPOSITIONS
a) Distinction between the Traditional and Modern General propositions.
b) Meaning of prediction with special reference to the Copula.
c) Failure of Traditional classification of propositions.

a) Distinction between the Traditional and Modern General propositions.

According to Traditional Logic general propositions are classified in four categories.

These are:

A = Universal affirmative

E = Universal negative

I = Particular affirmative

O = Particular negative

We have already studied them in details in earlier chapters.

General Propositions in modern Logic are similar to those in traditional logic.

‘All mobile phones are electronic gadgets’ is simple proposition. In such proposition we find the relation of different classes.

In the above proposition the subject term refers to a class of objects ‘mobile phones’ & the predicate term refers to another class of objects ‘electronic gadgets’.

So, a general proposition is a proposition which asserts that one class is wholly or partly included in or excluded from another class.

A general proposition, therefore, makes an assertion about all or about some of the members of a class.

The method of symbolizing with Quantifiers, seen in chapters above is actually the method used in Modern Logic, after the concept of symbolizing the propositions became popular.

b) Meaning of prediction with special reference to the Copula.

Traditional logicians have divided propositions into singular and general. Singular propositions have a single individual as a subject. This means, in a singular proposition, the subject is a singular individual thing and predicate is a class of individuals.

General propositions have a group of individuals as a subject. This means, in a General proposition, we have a group of individuals as a subject as well as a group of individuals as a predicate.

The general propositions are of two types, universal and general.

When the general proposition says something about the entire group indicated in the subject, it is known as a universal proposition.

When the general proposition says something about a part of the group indicated in the subject, it is known as a particular proposition.

Both singular and general propositions are either affirmative or negative. When we are told that the subject has the quality indicated in the predicate, the proposition is said to be affirmative. When we are told that the subject does not have the quality indicated in the predicate, the proposition is said to be negative.

In case of affirmative propositions, in singular proposition, the quality indicated in the group stated in the predicate is applicable to the individual indicated in the subject, while in general proposition, it either is applicable to the entire group indicated by the subject, as in universal propositions, or to a part of the group indicated by the subject, as in particular propositions.

In case of negative propositions, in singular proposition, the quality indicated in the group stated in the predicate is not applicable to the individual indicated in the subject, while in general proposition, it is either not applicable to the entire group indicated by the subject, as in universal propositions, or not applicable to a part of the group indicated by the subject, as in particular propositions.

According to this, the general propositions are classified into four categories.

These are:

A = Universal affirmative

E = Universal negative

I = Particular affirmative

O = Particular negative

c) Failure of Traditional classification of propositions.

The problem of multiple generality names a failure in traditional logic to describe certain intuitively valid inferences. For example, it is intuitively clear that if:

“Some cat is feared by every mouse”

then it follows logically that:

All mice are afraid of at least one cat

The syntax of traditional logic (TL) permits exactly four sentence types:

"All As are Bs",

"No As are Bs",

"Some As are Bs" and

"Some As are not Bs".

Each type is a quantified sentence containing exactly one quantifier.

Since the sentences above each contain two quantifiers; 'some' and 'every' in the first sentence and 'all' and 'at least one' in the second sentence, they cannot be adequately represented in TL.

The best TL can do is to incorporate the second quantifier from each sentence into the second term, thus rendering the artificial-sounding terms 'feared-by-every-mouse' and 'afraid-of-at-least-one-cat'. This in effect "buries" these quantifiers, which are essential to the inference's validity, within the hyphenated terms.

Hence the sentence "Some cat is feared by every mouse" is allotted the same logical form as the sentence "Some cat is hungry". And so the logical form in TL is:

Some As are Bs

All Cs are Ds

which is clearly invalid.

The first logical calculus capable of dealing with such inferences was Gottlob Frege's Begriffsschrif, the ancestor of modern predicate logic, which dealt with quantifiers by means of variable bindings.

Modestly, Frege did not argue that his logic was more expressive than extant logical calculi, but commentators on Frege's logic regard this as one of his key achievements.

Using modern predicate calculus, we quickly discover that the statement is ambiguous.

Some cat is feared by every mouse

could mean

Some cat is feared by every mouse, i.e.

For every mouse m, there exists a cat c, such that c is feared by m,

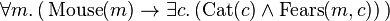
in which case the conclusion is trivial.

But it could also mean Some cat is (feared by every mouse), i.e.

There exists one cat c, such that for every mouse m, c is feared by m.

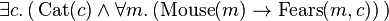
This example illustrates the importance of specifying the scope of quantifiers as for all and there exists.